Vectors
- A vector has both magnitude and direction but a scalar has only magnitude
- Example of a scalar is Temperature
- Example of a vector is Acceleration
- A vector can be moved around (slide sideways, slide up or down on a piece of paper) once its DIRECTION and LENGTH are NOT altered
- Because of the above, vectors can be arranged "head to tail" graphically (geometrically) to find their SUM (the vector sum is also a vector and called the RESULTANT)
- Two vectors can also be arranged "tail to tail" and the smallest angle between them found to obtain the DOT PRODUCT and the CROSS PRODUCT
Vector Algebra
Vector Direction and Vector Display Modes
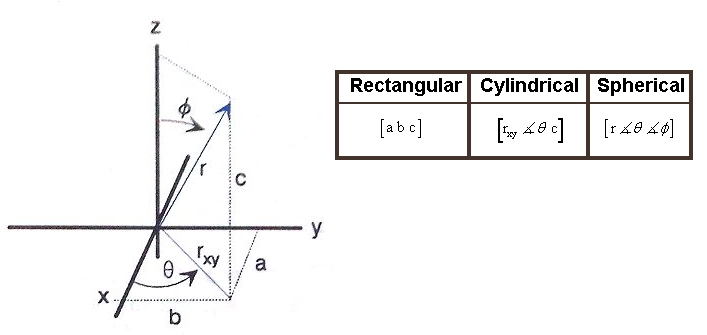
Converting between Vector 3-Dimensional Display Modes
Rectangular to Cylindrical
Rectangular to Spherical
Cylindrical to Rectangular
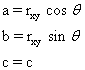
Cylindrical to Spherical
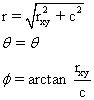
Spherical to Rectangular
Spherical to Cylindrical
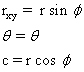
Vector Multiplication
A vector can be multiplied by a scalar... and this gives a new vector with a magnitude the product of the original vector and scalar
and the same direction (if scalar is positive) or reverse direction (if scalar is negative)
Division by a scalar is accomplished by taking the reciprocal of the scalar and multiplying as above.
A scalar product (DOT product) of two vectors is obtained by:
and a vector product (CROSS product) of two vectors is obtained by:
Vector components, Unit Vectors of the Cartesian (Rectangular) coordinate system
It is usual to specify vectors by their components on a coordinate system
and the vector components of a rectangular coordinate system are related to each other by only two angles,
zero or 90 degrees, therefore their cosine (or sine) values are either zero or one,
and this produces the following cases for the DOT and CROSS products of the unit vector components
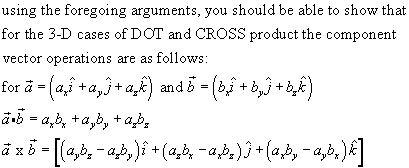
© copyright 2010 Stephen E. Mendes, Barbados.
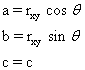
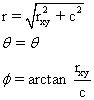
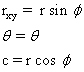
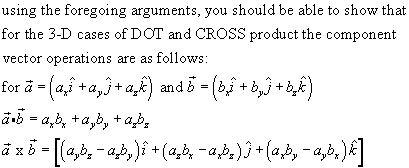
P10C Homepage